Cela peut paraître curieux, concernant un établissement qui se veut progressiste et bienveillant comme l’Institut intergalactique, mais le bâtiment est doté d’un cachot. Point de murs en pierre suintant l’humidité éclairés par la lumière blafarde de torches vacillantes, point de chaînes en fer, de remugles de douves et autres rats aux dents rougies que l’on associe traditionnellement à ce genre de lieu ; la pièce ressemble plutôt à une salle de classe qui, étant située au sous-sol, a vu ses fenêtres remplacées par un soupirail. Mais dans l’esprit des étudiants, il s’agit bel et bien d’un cachot. On y trouve, d’ailleurs, des instruments de torture.
Le cachot est présentement occupé par le malheureux Bêta, qui y a été conduit par un professeur Phi furieux : non content de s’être assoupi pendant le cours de mathémagie, le jeune étudiant a manqué d’à propos en assénant un « Laisse-moi dormir, maman » à son enseignant lorsque ce dernier a tenté de lui faire quitter les bras de Morphée. Vexé d’être assimilé à une figure maternelle, le professeur Phi, lui-même pas spécialement adepte du progressisme et de la bienveillance, a condamné son élève au cachot…
Le prix de la liberté
Après y avoir conduit Bêta, Phi a ouvert l’armoire qui contient les instruments de torture et en a tiré un objet en plastique.
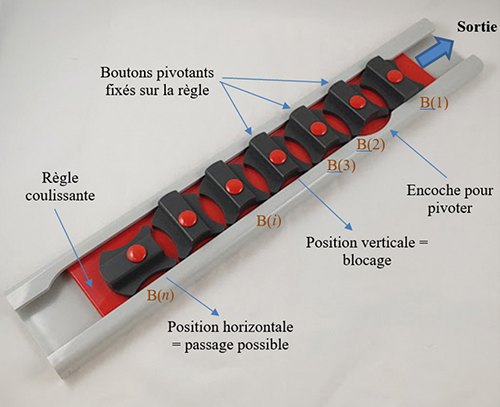
« Monsieur Bêta, a-t-il déclaré, vous avez le choix : soit vous me libérez entièrement cette règle sans rien casser, soit vous me calculez le nombre de manipulations nécessaires pour y arriver. Après, seulement, vous aurez le droit de sortir. »
Cela fait déjà une demi-heure que Bêta s’acharne sur le casse-tête quand le visage de sa camarade Epsilon apparaît au niveau du soupirail.
« Aide-moi, la supplie-t-il, ou je vais rester enfermé ici pendant des siècles ! Je ne sais pas comment je me suis débrouillé, mais je suis revenu à la position de départ où tous les boutons sont verticaux et bloquent cette fichue règle… Comment faire pour tous les passer à l’horizontale, dans quel ordre les manipuler ? »
Epsilon observe le casse-tête et propose : « Formalisons un peu tout cela. S’il n’y avait qu’un seul bouton, il suffirait de le faire pivoter, tu t’en sortirais avec un mouvement.
– Mouvement ? Qu’est-ce que tu comptes ? Les boutons pivotent, la règle coulisse…
– Je ne compte que le nombre de boutons que je fais pivoter, je ne compte pas les opérations de déplacement de la réglette. Avec deux boutons, tu pourrais faire pivoter
B (1) puis B (2) et on serait bons avec deux mouvements. Avec trois boutons, tu dois commencer par faire pivoter B (1), puis tirer la règle jusqu’à pouvoir faire pivoter B (3). Si tu fais pivoter B (2) à ce moment, c’est fichu. Donc tu bouges la règle pour refaire pivoter B (1), puis B (2), puis B (1) et c’est terminé. On a donc cinq mouvements. On peut en fait décrire une procédure Pr (n) qui permet d’inverser la position de tous les boutons, n étant le nombre de boutons :
Si n = 1, alors pivote B (1) ;
Si n = 2, alors pivote B (1) et B (2) ;
Sinon :
Pr (n – 2),
Pivote B (n),
Pr (n – 2),
Pr (n – 1).
– Ok, compris, lance Bêta tout en manipulant le casse-tête. Je devrais m’en sortir avec cette information ! Tu m’as sauvé la vie !
– Attends ! s’alarme Epsilon, c’est beaucoup plus intéressant de pousser la théorie plus loin et de trouver une formule qui donne le nombre de manipulations à faire pour dégager la règle, en fonction de la quantité de boutons ! La procédure permet de trouver une relation de récurrence, et en traitant différemment les cas pairs et impairs… »
Mais Bêta, en route vers la liberté, ne l’écoute déjà plus.
Et vous, cher lecteur, sauriez-vous trouver la formule qui donne le nombre de boutons à manipuler en fonction de leur nombre pour dégager la règle ?

