
Le mathématicien hongrois Paul Erdős (1913–1996).
Si l’on considère n points du plan, on peut leur associer n (n – 1)/2 distances en les prenant tous deux à deux. Parmi ces n (n – 1) / 2 distances, combien au maximum peuvent être égales à 1 ? Désignons ce nombre maximum par f (n). Voici les valeurs de f (n) pour les premières valeurs de n.

On construit facilement les configurations correspondantes en choisissant les points sur un réseau à mailles triangulaires (le cas de sept points correspond aux sommets et au centre d’un hexagone régulier de côté 1).
Un problème différent consiste à chercher le nombre minimal de distances distinctes déterminées par n points du plan. Appelons g (n) ce nombre minimal ; en voici les premières valeurs.

On peut alors chercher les configurations correspondant à chaque valeur de n. Pour n = 3, il s’agit évidemment des sommets d’un triangle équilatéral. Pour n = 4, les sommets d’un carré constituent une solution, mais il en existe bien d’autres (par exemple en prenant les sommets de deux triangles équilatéraux de même côté assemblés par un côté). Pour n = 5, il existe une seule configuration, à savoir les sommets d’un pentagone régulier. Pour n = 6, les sommets d’un hexagone régulier donnent une solution permettant de définir exactement trois distances différentes.
1. Il existe d’autres configurations de six points définissant seulement trois distances différentes. Saurez-vous les retrouver ?
Toujours dans le plan…
Des nombres d’occurrences de chaque distance tous différents ?
Voici un troisième problème proposé par Erdős. À un ensemble de n points correspondent n (n – 1) / 2 paires de points. Or on sait que n (n – 1) / 2 est égal à la somme des n – 1 premiers entiers strictement positifs. D’où l’idée du problème suivant : dans un ensemble de n points du plan tels que trois d’entre eux ne soient jamais alignés et que quatre d’entre eux ne soient jamais situés sur un même cercle, est-il possible qu’une distance d1 n’apparaisse qu’une seule fois, une distance d2 exactement deux fois… une distance dn–2 exactement n – 2 fois et une distance dn–1 exactement n – 1 fois ?
On connaît des exemples pour 2 ≤ n ≤ 8, et rien au-delà. Erdős a proposé une récompense pour une preuve d’impossibilité au-delà d’une certaine valeur de n ou pour des exemples pour n arbitrairement grand, mais le problème reste non résolu.
Pour n = 3, le cas des sommets d’un triangle isocèle non équilatéral fait l’affaire. Pour 4 ≤ n ≤ 8, de nombreux exemples ont été construits. La mathématicienne hongroise Ilona Palasti (1924–1991) a proposé des configurations de points placés sur un réseau à mailles triangulaires.
Voici sa solution pour huit points. L’unité de longueur étant le côté des mailles du réseau triangulaire, on a :
AG = AD = CG = CH = DG = FH = FC = ,
AF = BE = ED = DH = EH = BD = ,
AB = CD = EG = GF = FE = 2,
AC = CE = EA = GH = ,
FD = GB = HB = ,
FB = AH = ,
BC = 1.
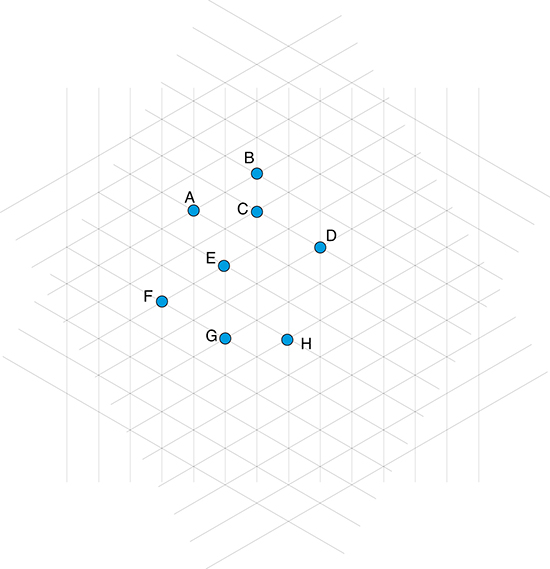
2. Saurez-vous construire de telles configurations de n points pour 4 ≤ n ≤ 7 ?
On peut aussi se poser ces mêmes questions dans l’espace à trois dimensions. Avis aux amateurs de géométrie combinatoire !
SOURCES
• Unsolved Problems in geometry. Hallard Croft, Kenneth Falconer et Richard Guy, Springer, 1991.
• Lattice-points examples for a question of Erdős. Ilona Palasti, Periodica Mathematica Hungarica 20, 1989.

