« Ces urbanistes sont des idiots ! »
Quelques têtes se tournent en direction du professeur Phi, qui vient de lancer cette affirmation péremptoire à la cantonade. Et parce qu’à l’Institut intergalactique la cantonade a d’autres préoccupations que les vociférations coutumières de son enseignant de mathémagie, elle s’en retourne bien vite à ses travaux habituels – ce qui ne manque pas d’accroître l’énervement du professeur en question.
« L’argent de nos impôts part dans des dépenses non optimisées et je suis le seul à m’en offusquer ! Quelle honte !
– Ça ne doit pas être top pour votre tension de vous énerver ainsi, ose lui glisser son élève Bêta. Quel crime de lèse-mathématique a donc bien pu commettre cette caste qui s’occupe de nos villes et de nos routes pour mériter ainsi votre opprobre et votre courroux ? »
Le ton ironique de la question parvient à échapper totalement au professeur aveuglé par l’indignation : « Ces olibrius avaient pour mission de relier, par une fort coûteuse voie rapide à lévitation magnétique, quatre villes disposées en carré. Et vous savez comment ils ont fait ? Comme ceci ! »
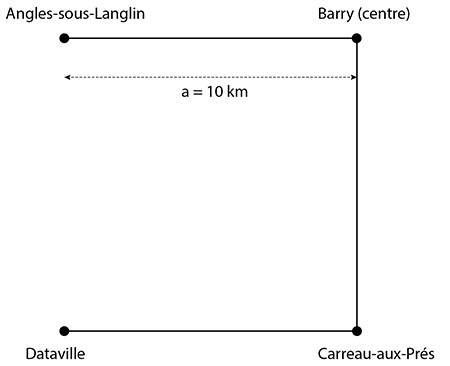
Où part l’argent des impôts…
Bêta observe la figure en se grattant le menton : « Pas très judicieux, en effet. Ils ont dû construire 3a = 30 km de voie rapide. Alors qu’ils auraient été bien plus inspirés de faire comme cela. Pythagore nous fait dire qu’on n’a besoin dans ce cas que de soit 28,28 km d’installation. »
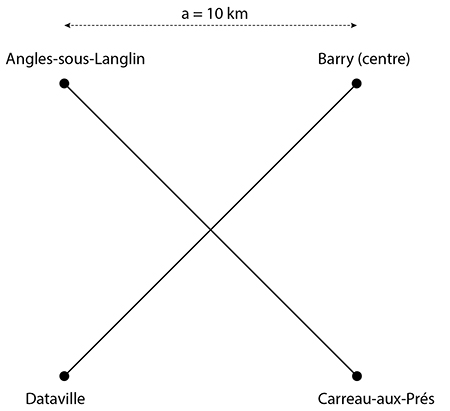
« Mais vous êtes presque aussi idiot que ces bons à rien ! rugit le professeur Phi. Voilà évidemment ce qu’il aurait fallu faire. »
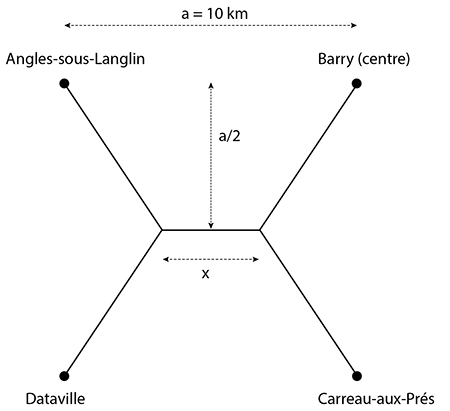
« Il y a une inconnue dans votre projet, fait remarquer Bêta.
– Vous ne pensiez tout de même pas que j’allais faire tout le travail à votre place, grince le professeur Phi. Allez, au boulot ! »
Eh oui, au boulot, cher lecteur ! Quelle valeur de x permet de minimiser la distance à parcourir pour relier les villes deux à deux ?
« Je ne suis pas sûr de savoir comment procéder, s’interroge Bêta, qui commence à regretter de s’être lancé dans la discussion.
– Si vous écoutiez mes cours au lieu de bâiller et de bayer aux corneilles, vous sauriez comment calculer la taille du réseau en fonction de x, puis dériver cette fonction par rapport à x pour voir quand elle s’annule afin de rechercher son minimum. Et avec un peu de résolution d’équations du second degré et de rigueur, vous auriez déjà votre réponse ! »

