On pourrait penser que la résolution de problèmes d’autoréférence ne peut se faire que par tâtonnements inspirés. Il existe pourtant une méthode qui peut permettre, dans certains cas, de trouver une solution, même si ce procédé n’est absolument pas infaillible. Cette méthode s’apparente à une procédure pratiquée depuis l’Antiquité pour résoudre des problèmes d’arithmétique sans utiliser le calcul algébrique. Il s’agit de la méthode dite de la fausse position, qui consiste à proposer une solution quelconque, généralement fausse, avant d’ajuster le tir pour arriver à un résultat correct. L’erreur est ici volontaire, car elle permet de trouver la vérité.
Commençons par un exemple tout simple où on demande de compléter la phrase écrite dans le cadre avec des nombres écrits en chiffres.
|
Dans ce cadre, on compte exactement : • ...... multiple(s) de 2 ; • ...... multiple(s) de 3 ; • ...... multiple(s) de 4 ; • ...... multiple(s) de 5. |
On commence par compléter le cadre avec des nombres quelconques, par exemple :
|
Dans ce cadre, on compte exactement : • 2 multiple(s) de 2 ; • 2 multiple(s) de 3 ; • 2 multiple(s) de 4 ; • 2 multiple(s) de 5. |
La phrase est évidemment fausse, donc on la corrige en comptant le nombre de multiples de chaque sorte, en notant ces nombres dans un nouveau cadre, puis en recorrigeant le cadre précédent tant que la phrase n’est pas vraie :
|
6 mult. de 2 1 mult. de 3 1 mult. de 4 1 mult. de 5 |
3 mult. de 2 2 mult. de 3 1 mult. de 4 1 mult. de 5 |
3 mult. de 2 2 mult. de 3 1 mult. de 4 1 mult. de 5 |
La dernière colonne étant identique à celle qui précède, on peut affirmer que la phrase contenue dans le cadre est vraie et que l’on a obtenu une solution du problème.
On peut comparer cette situation à celle d’un point fixe, notion qui intervient dans de nombreuses branches des mathématiques. Si une fonction f définie et continue sur un certain intervalle possède un point fixe x, alors celui-ci vérifie l’égalité f (x) = x.
Mais la solution obtenue est-elle la seule ? Rien ne permet de l’affirmer...
1. Trouver une autre solution à ce problème.
Une autre question se pose : tout remplissage initial conduit-il à une solution en appliquant cette méthode ? Ici encore, rien n’est moins sûr. Démarrons avec un problème du même type auquel nous appliquons un (faux) remplissage initial :
|
Dans ce cadre, on compte • 1 chiffre(s) 0 ; • 2 chiffre(s) 1 ; • 2 chiffre(s) 2 ; • 2 chiffre(s) 3 ; • 2 chiffre(s) 4 ; • 1 chiffre(s) 5. |
• 1 chif. 0 ; • 3 chif. 1 ; • 5 chif. 2 ; • 1 chif. 3 ; • 1 chif. 4 ; • 1 chif. 5. |
• 1 chif. 0 ; • 5 chif. 1 ; • 1 chif. 2 ; • 2 chif. 3 ; • 1 chif. 4 ; • 2 chif. 5. |
|
• 1 chif. 0 ; • 4 chif. 1 ; • 3 chif. 2 ; • 1 chif. 3 ; • 1 chif. 4 ; • 2 chif. 5. |
• 1 chif. 0 ; • 4 chif. 1 ; • 2 chif. 2 ; • 2 chif. 3 ; • 2 chif. 4 ; • 1 chif. 5. |
• 1 chif. 0 ; • 4 chif. 1 ; • 3 chif. 2 ; • 1 chif. 3 ; • 1 chif. 4 ; • 2 chif. 5. |
• 1 chif. 0 ; • 4 chif. 1 ; • 2 chif. 2 ; • 2 chif. 3 ; • 2 chif. 4 ; • 1 chif. 5. |
Après quelques étapes, on retrouve un remplissage déjà rencontré ; malheureusement, il ne s’agit pas ici d’un « point fixe », mais d’une alternance infinie de deux remplissages du cadre (ici en vert et en orange).
Cela signifie-t-il que le problème n’a pas de solution ? Nullement...
2. Trouver une solution à ce problème.
Pour finir, voici une énigme un peu plus complexe. Il s’agit, ici encore, de compléter les deux phrases afin qu’elles soient simultanément vraies.
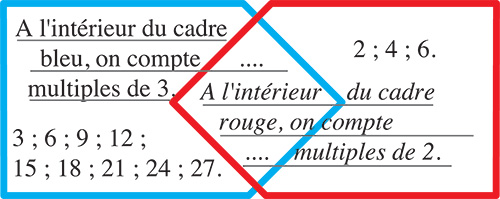
3. Trouver un remplissage de ce cadre qui rende la phrase vraie. Et même un deuxième !
SOURCES
- Gödel, Escher, Bach, les brins d’une guirlande éternelle. Douglas Hofstadter, Interéditions, 1996.
- Je suis une boucle étrange. Douglas Hofstadter, Dunod, 2021.

