La soucoupe sur la nappe
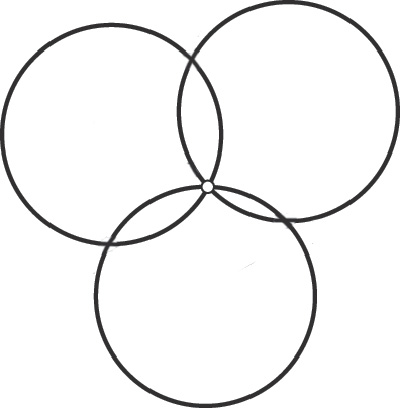
Au café, s’il y a une nappe en papier, j’aime bien poser le problème de Johnson : avec une soucoupe ronde, je trace trois cercles se coupant en un même point.
On y voit trois autres points d’intersection de ces cercles deux à deux, et un fait à la fois étonnant et remarquable que l’on peut vérifier « à la soucoupe » : le cercle circonscrit à ces 3 points a le même rayon que les trois premiers ! Pourquoi donc ?
Un peu d’aires…
Un rectangle est divisé en quatre rectangles plus petits, comme sur la figure. On connaît les aires de trois d’entre eux : 3, 4 et 5.
Quelle est l’aire du quatrième rectangle ?

Un simple puzzle à deux pièces
Placer ces deux pièces l’une à côté de l’autre de manière à ce que la figure formée présente un axe de symétrie (le lecteur pourra essayer de résoudre le puzzle en décalquant les pièces).

André Deledicq (né en 1943) est bien connu de plusieurs générations (au sens scolaire !) d’élèves et de professeurs puisqu’il est à l’origine du concours Kangourou qu’il a créé en 1991 avec Jean-Pierre Boudine et pour lequel il a reçu le prix d’Alembert en 1994 et le prix Erdős en 2004.
Les mathématiques lui ont toujours procuré une intense jubilation. Et il n’a eu de cesse de la faire partager au plus grand nombre de jeunes et de moins jeunes. Enseignant-chercheur à l’université Paris 7 (aujourd’hui Paris Cité), il y a travaillé dans plusieurs champs des mathématiques (entre autres le contrôle optimal, l’histoire des mathématiques et l’analyse non-standard) et a participé aux actions du premier IREM de France, à Paris, qu’il a par la suite dirigé. Fortement investi dans la formation des enseignants, il a exercé des responsabilités importantes dans ce domaine. Auteur très prolifique, André Deledicq s’est rapidement imposé comme un des grands vulgarisateurs des mathématiques, en France et dans le monde.
Le problème de la soucoupe est, pour lui, caractéristique de ces questions qui font apparaître des choses cachées dans leur solution : « la démonstration est élémentaire et cache une figure bien connue : un cube. » Le problème de l’aire est extrait du concours Kangourou 6e-5e de 1996 : « il n’est en fait pas si facile que ça et on se demande vraiment comment faire. » Dans la série des défis qui, curieusement, ne sont pas résolus aussi vite qu’ils le devraient, le troisième est le plus impressionnant : « Le puzzle m’a été offert par François Célérier (www.jeux-efce.com). Il est constitué de deux pièces seulement ; il n’y a pas plus simple ! Et les pièces ne sont pas très compliquées : ce sont deux polygones à cinq côtés. Normalement ce puzzle ne devrait pas être difficile : on ne peut qu’essayer de placer l’un des côtés de l’une des pièces le long d’un des cinq côtés de l’autre (et on voit vite qu’aucun des côtés rentrants ne peut servir). En fait, cela ne fait que neuf possibilités à essayer ! Comment se fait-il que beaucoup de gens mettent beaucoup de temps à trouver la solution ? »


