Dattatreya Ramachandra Kaprekar (1905-1986) est un enseignant indien qui passa sa vie à effectuer des recherches sur les nombres entiers, recherches qu’il présentait lors des congrès annuels des associations mathématiques indiennes. La plupart de ses travaux sont liés à l’écriture décimale des nombres.
La constante de Kaprekar
La publication la plus connue de Kaprekar, qui fut ensuite popularisée par Martin Gardner dans une de ses chroniques du Scientific American, est celle concernant un algorithme sur les nombres entiers d’au plus quatre chiffres, qui aboutit à un « puits », en l’occurence le nombre 6174, connu sous le nom de « constante de Kaprekar ».
L’algorithme fonctionne de la façon suivante. À partir d’un nombre de quatre chiffres non tous égaux, on réordonne ses chiffres du plus grand au plus petit, puis on retourne l’ordre des chiffres du nombre obtenu (l’écriture de ce nombre retourné peut alors commencer par un zéro), et on soustrait le plus petit du plus grand.
En partant par exemple du nombre 7442, on effectue 7442 − 2447 = 4995, puis on recommence : 9954 − 4599 = 5355. Kaprekar a montré qu’en partant de n’importe quel nombre à quatre chiffres non tous égaux, on aboutit en au plus sept opérations au nombre 6174, qui vérifie 7641 − 1467 = 6174.
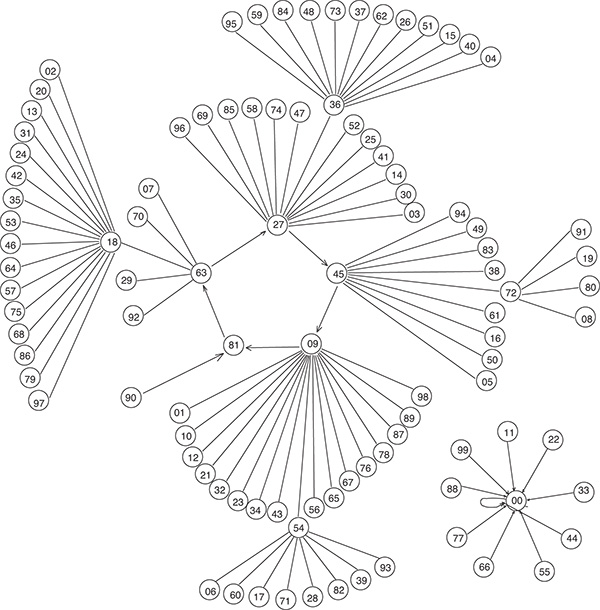
On a pu également étudier cet algorithme sur des nombres à trois chiffres non tous égaux (on a alors un puits avec le nombre 495) ou sur des nombres à deux chiffres différents (on a alors un cycle de 5 nombres : 09 – 81 – 63 – 27 – 45).
Retourner sans ordonner
La première publication de Kaprekar à propos de 6174 date de 1946, mais il explora bien d’autres pistes. Dans une variante de son algorithme, il ne réordonne pas les chiffres, mais retourne simplement l’écriture du nombre avant de soustraire le plus petit du plus grand. Le nombre d’écritures à quatre chiffres étant fini, on sait qu’on aboutira à un puits ou à un cycle. Testons l’algorithme en partant de 6174 par exemple. Ici encore, on autorise le zéro comme premier chiffre.
La première étape est donc 6174 − 4716 = 1458. On recommence : 8541 − 1458 = 7083. Puis 7083 - 3807 = 3276. On laisse le lecteur continuer les calculs pour trouver les résultats successifs qui sont 3447, 3996, 2997, 4995, 0999, 8991, 6993, 2997.
On constate qu’on arrive à un cycle de cinq nombres :
2997 – 4995 – 0999 – 8991 – 6993 qui va se répéter indéfiniment.
Kaprekar a cartographié l’ensemble des 10 000 nombres de 0000 à 9999, et il a montré qu’en dehors du puits 0000, il existait trois cycles de cinq nombres et un cycle de deux nombres. Le fait que ces cycles comportent tous deux ou cinq nombres est sans doute lié au système de numération décimale.
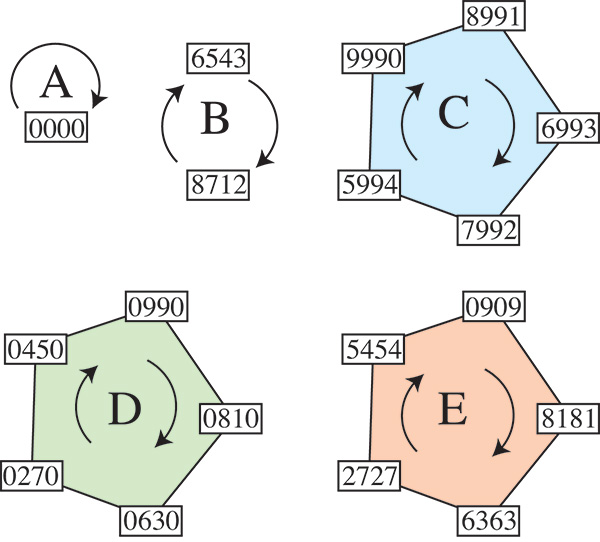
1 - En partant de 2025, à quel puits ou cycle arriverez-vous ?
Kaprekar a montré que le cycle auquel aboutit un nombre quelconque à quatre chiffres abcd dépend uniquement des différences a − d et b − c.
Il est immédiat que si a − d = b − c = 0, on a affaire à un nombre palindrome qui aboutit au puits A.
Dans les autres cas, les nombres se répartissent entre les cycles en fonction de ces différences.
2 - À quel cycle conduira un nombre à 4 chiffres qui s’écrirait ab (b − 3) (a − 4),
avec 4 ≤ a ≤ 9 et 3 ≤ b ≤ 9 ? Un nombre de la forme a (b − 3) b (a − 4) aboutirait-il au même cycle ?

