Personne ne le contestera : un bon graphique peut très souvent constituer un support appréciable à la démonstration d’un théorème ou d’une propriété. Il y a même des cas pour lesquels le ou les graphiques considérés contiennent en fait une certaine forme de démonstration de la propriété.
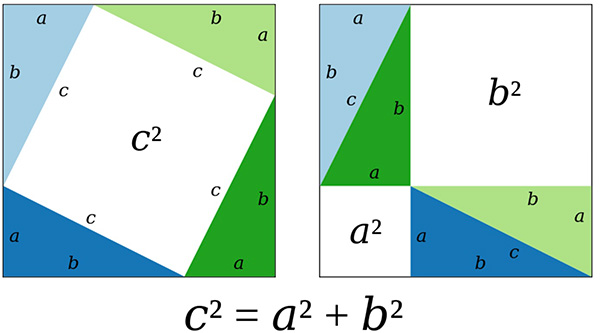
L’exemple le plus connu de ce type de situation est celui du théorème de Pythagore pour lequel la double représentation graphique ci-contre contient effectivement ce qui peut être considéré comme une preuve du résultat. Un graphique bien construit peut également conduire sans autre considération à la formule des sinus et cosinus de sommes d’angles.
Mais jusqu’où peut-on faire confiance à une représentation graphique ? Dans quelle mesure notre œil peut-il ou non se laisser berner par une apparence qui pourrait être trompeuse ?
Le carré manquant
Considérons par exemple le cas d’une carré de 8 unités sur 8 que l’on décompose en deux triangles et deux trapèzes isométriques. En réajustant les pièces, on peut reconstituer ce qui ressemble alors à un rectangle. Problème : l’aire du carré est de 64 unités de surface, celle du rectangle de 65 unités. Ce paradoxe généralement associé au mathématicien Charles Lutwidge Dodgson, mieux connu sous le pseudonyme de ... Lire la suite
