
En géométrie élémentaire on s’intéresse très vite à l’ensemble des points à égale distance de deux points A et B donnés : c’est la médiatrice du segment [AB]. À peine cette notion définie, on s’empresse en général d’énoncer le théorème selon lequel la médiatrice est la perpendiculaire à la droite (AB) passant par le milieu de [AB].
On introduit presque aussi vite l’ensemble des points à égale distance de deux droites, ou plutôt à deux demi-droites de même origine S, ce qui correspond à la bissectrice du secteur angulaire ainsi défini. (En pratique on part plutôt du point de vue inverse, en commençant par définir la notion de bissectrice d’un angle pour ensuite démontrer qu’il s’agit de l’ensemble des points à égale distance de ses deux côtés.)
Points à égale distance de deux points, points à égale distance de deux droites… une façon somme toute assez naturelle de chercher du neuf consiste alors à s’intéresser aux points à égale distance d’un point et d’une droite. C’est là qu’apparaît la parabole.
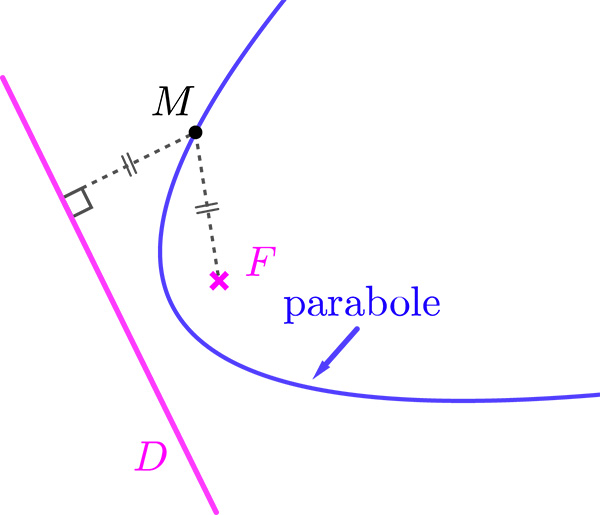
Par définition, un point F et une droite D étant donnés, la parabole de foyer F et de directrice D est l’ensemble des points M du plan tels que MF = d(M, D), où ... Lire la suite
