
Vous avez déjà certainement lancé une boule de pétanque. La plupart du temps, la trajectoire suivie par la boule est assez proche d’une parabole. En effet, en négligeant les frottements et dans un champ de pesanteur uniforme, les coordonnées du projectile tiré avec une vitesse initiale v0 et un angle α vérifient z = (tan α) x – g2 v02 cos2(α) x2. Cette jolie formule s’applique aussi pour des boulets de canon ou, plus pacifiquement, des feux d’artifices ou des jets de fontaines. On peut alors en déduire que la distance de tir est de v02 g sin(2α) et est donc maximale pour un angle de tir de 45°. La hauteur de tir est quant à elle égale à v02 2g sin2(α). Plus intéressant encore, toutes ces paraboles sont enveloppées par une autre, la parabole dite de sûreté, d’équation z = v02 2g – 2gv02 x2, et dont le foyer n’est autre que le point de tir. Dans l’espace, on obtient bien sûr un paraboloïde de sûreté. Dans le monde réel, les frottements dus à l’air ne sont pas toujours aussi négligeables qu’on le souhaiterait. Dans ce cas, les courbes obtenues sont des « paraboles amorties » qui ne sont justement pas des paraboles mais des courbes transcendantes.
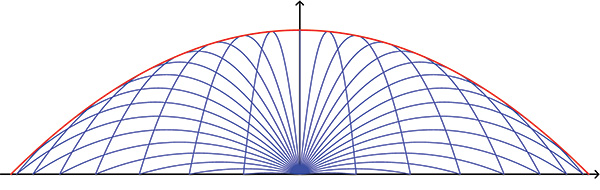
Toutes les trajectoires obtenues avec la même vitesse initiale (sans frottement) sont situées sous la parabole de sûreté.
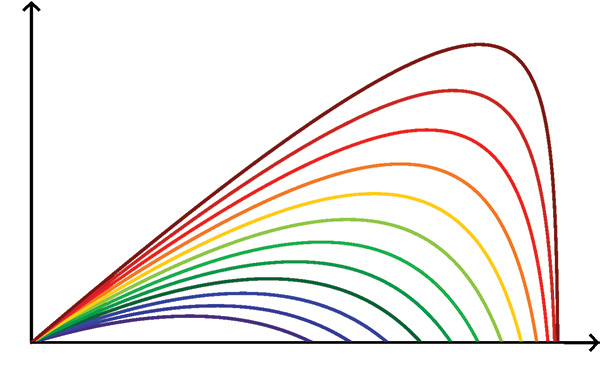
Différentes paraboles amorties avec un coefficient de frottement plus ou moins important.
Un miroir liquide !
Placez un liquide dans un cylindre posé sur une de ses bases. Faites ensuite tourner ce cylindre autour de son axe à vitesse angulaire constante et observez : le liquide prend alors la forme d’un paraboloïde ! La propriété persiste quelle que soit la forme du fond. En faisant tourner un liquide réfléchissant comme le mercure, on peut ainsi obtenir un miroir parabolique parfait et construire un télescope à moindre coût. On dit qu’Isaac Newton (1643-1727) y avait déjà pensé en son temps, puis Ernesto Capocci (1798-1864) en 1856, mais il a fallu attendre plusieurs siècles pour que la technologie soit opérationnelle. Depuis, des miroirs de plus de 3 mètres de diamètre ont été réalisés. Le plus grand, mis hors service en 2016, atteignait les 6 mètres de diamètres (avec une vitesse angulaire de 8,5 tours par minutes) et était installé à 70 km de Vancouver.
Un atout architectural
Pour les architectes, la parabole est bien plus qu’une courbe abstraite, elle est une source d’inspiration, une matière avec laquelle jouer entre équilibre et lumière. C’est par exemple le cas pour Oscar Niemeyer (1907-2012) au début des années 1940 qui dit avoir voulu « tropicaliser » le style de Le Corbusier avec son église de Belo Horizonte, au Brésil. Son contemporain mexicain Félix Candela (1910-1997) a fait de la parabole sa signature. Santiago Calatrava Valls (né en 1951) a repris le flambeau en utilisant abondamment la parabole comme emblème visuel. D’un architecte à l’autre, la parabole relie rigueur géométrique et potentialité poétique.

