
Avec le cercle et l’ellipse, la parabole est une des courbes planes les plus simples qui soient. On peut la décrire comme un ensemble de points vérifiant une propriété géométrique facile à énoncer. Donnez-vous un point F et une droite Δ qui ne passe pas par F. L’ensemble des points à égale distance de F et de Δ forme une parabole (voir l'article « Une droite, un point, c’est tout »). Le point F en est le foyer et la droite Δ la directrice. Partir de cette définition permet d’explorer les propriétés de cette courbe géométriquement. On peut préférer une approche plus analytique. En choisissant convenablement son repère orthonormé, on peut considérer qu’une parabole est une courbe d’équation y = mx2 où m est un réel strictement positif. Dans ce cas, le foyer F a pour coordonnées et la directrice a pour équation
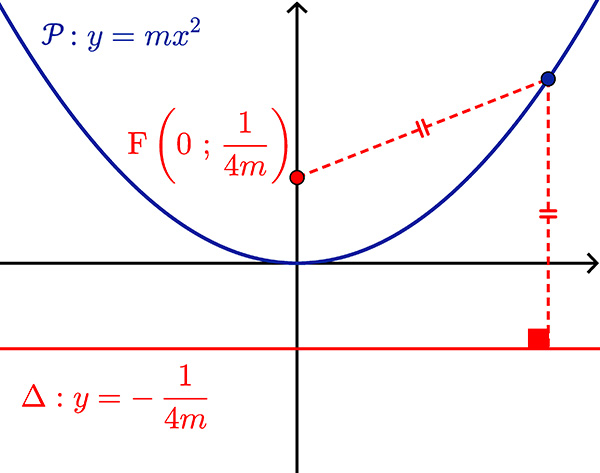
Dans un repère orthonormé bien choisi, la parabole de foyer F
et de directrice Δ a une équation simple : y = mx 2.
Des tangentes et des cordes
Voir les paraboles comme courbes d’une fonction polynôme du second ... Lire la suite
