
Il renoue ainsi avec l’approche de Girard Desargues (1591-1661) et Blaise Pascal (1623-1662) qui avait été délaissée durant deux siècles, écrasée par l’efficacité cartésienne. De retour en France, il publie en 1822 son Traité des propriétés projectives des figures. L’ellipse, l’hyperbole et la parabole ne sont alors plus que les mêmes visages d’une simple conique et le savant en étudie toutes les propriétés invariantes par transformations perspectives. Il introduit aussi la notion de dualité qui sera fortement développée ensuite. Ce nouveau regard porte en lui les germes d’un renouveau total de la géométrie, passant de l’étude des figures à l’étude des transformations.
Les deux théorèmes de Poncelet
La démarche de Poncelet permet de démontrer en toute généralité des propriétés qui s’interprètent de façon concrète dans le cadre de la géométrie habituelle.
Considérons donc une parabole de foyer F et deux points A et A' de cette parabole. Appelons M le point d’intersection des tangentes à
en A et A'. Le premier théorème de Poncelet permet d’affirmer que la droite (MF ) est alors une bissectrice de l’angle
.
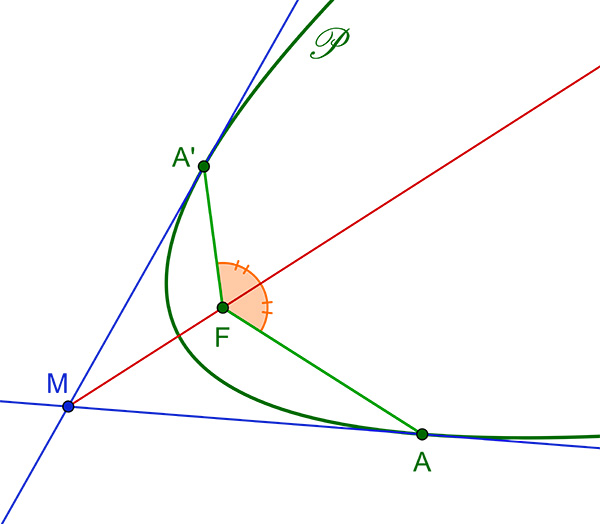
Le premier théorème de Poncelet dans le cas d’une parabole.
Appelons ... Lire la suite
