
Au IIIe siècle avant notre ère, Archimède se pose la question suivante : deux points U et V sur une parabole P étant donnés, quelle est l’aire de la surface comprise entre P et le segment [UV ] ?
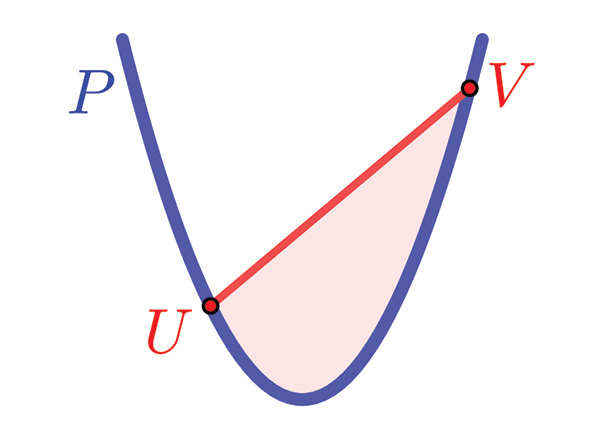
De nos jours, on a plutôt tendance à introduire la question « dans l’autre sens », c’est-à-dire à s’intéresser plutôt à l’aire en-dessous de la parabole (en introduisant des segments convenables), mais il est facile de voir que les deux versions sont fondamentalement équivalentes.
Dans l’Antiquité, la géométrie n’utilise pas la notion de repère si commune aujourd’hui, et l’idée même que la parabole peut être vue non comme une ligne mais comme la courbe représentative d’une fonction n’est pas du tout à l’ordre du jour. Les démonstrations mathématiques doivent donc trouver des voies qui nous semblent assez complexes, mais qui ne manquent pas d’élégance et sont aussi parfois l’occasion de mettre en évidence certaines propriétés inattendues. La principale d’entre elles pour une quadrature de la parabole « à l’antique » est la suivante. Une parabole P étant donnée, appelons milieu parabolique (la dénomination n’est pas standard, nous l’introduisons ici faute d’expression consacrée) de deux points U et V sur P le point I = m(U, V ) obtenu en ... Lire la suite
