La géométrie euclidienne (300 avant J.C.) repose sur des définitions d’objets géométriques (points, droites, etc.) et sur cinq postulats, règles de base pour travailler avec ces objets. Le premier postulat affirme par exemple qu’un segment peut toujours être tracé en joignant deux points quelconques. Le cinquième, plus complexe, implique que pour toute droite, par tout point n’appartenant pas à cette droite, il passe une unique parallèle à la droite. Ici des droites sont dites parallèles si leur intersection est vide.
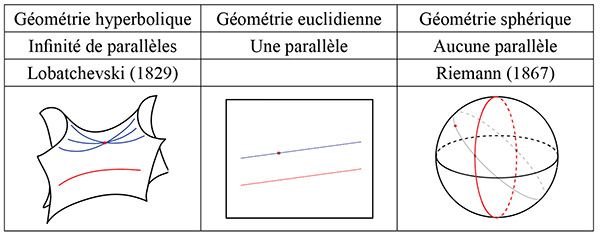
Ce cinquième postulat a longtemps posé question : peut-il se déduire des quatre précédents ? Finalement au XIXe siècle, il a été démontré qu’il était bien indépendant. De cette constatation ont émergé deux nouveaux types de géométries, qui se distinguent de la géométrie euclidienne par le remplacement de ce postulat. En géométrie hyperbolique par exemple, par un point il passe une infinité de parallèles à une droite donnée. Pour rendre ceci formel, il faut redéfinir la notion de droite et sortir du cadre du plan euclidien : c’est le but de la suite.
Surfaces, distances et géodésiques
En mathématiques, une surface est un objet qui de près ressemble à un plan, de la même manière que la Terre semble plate ... Lire la suite
