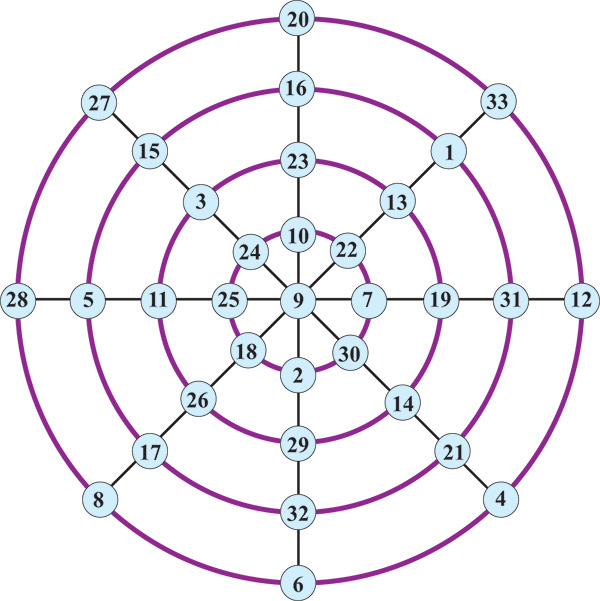
Les cercles magiques suivants sont dus au mathématicien japonais Seki Kowa (ou Seki Takakazu, vers 1640-1708, voir l'article « Le wasan ou les mathématiques de l'époque d'Edo »). Ils contiennent les nombres entiers de 1 à 33 et présentent une somme des nombres écrits sur chacun des cercles égale à 138 et une somme des nombres écrits sur chacun des diamètres égale à 147.
Construire des cercles magiques à partir d’un carré magique
Le premier carré magique, connu sous le nom de « diagramme des neuf palais » (en japonais) ou lo shu (en chinois) est un carré magique dit normal, d’ordre 3 (il contient les entiers de 1 à 9) et il présente la même somme sur les lignes, les colonnes et les deux diagonales.
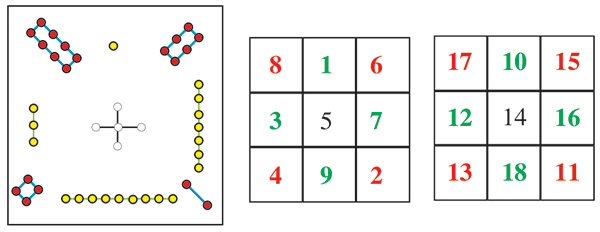
Si on adjoint à ce carré magique un second carré dans lequel on a augmenté tous les nombres du premier carré de 9 unités (il contiendra alors les entiers de 10 à 18), en disposant les 18 nombres sur les intersections de trois cercles concentriques avec trois diamètres communs à ces cercles, on obtient une figure magique présentant la même somme, égale à 57, sur les trois cercles et les trois diamètres.
Il faut noter que dans chacun des deux carrés initiaux, on pouvait échanger deux lignes ou deux colonnes quelconques sans affecter la magie des lignes ou des colonnes. Dans les cercles magiques, deux nombres placés dans deux cases de même couleur et de même teinte (claire, intermédiaire ou foncée) ont toujours la même somme, égale à 19. Deux tels nombres peuvent donc être échangés sans détruire les propriétés magiques de la construction. Cette possibilité permet de générer quantité de figures dans lesquelles les petits nombres et les grands nombres seront mieux répartis.
On n’a pas ici de nombre central comme dans le cercle de Seki Kowa, sauf si on y ajoute le nombre 0. On pourrait également placer au centre le nombre 10 (en ajoutant 1 à tous les nombres du second carré) ou le nombre 33, mais les sommes des cercles et celles des diamètres seraient alors différentes.
Avec des rectangles magiques
La construction de cercles magiques peut également être réalisée à partir de rectangles magiques. Un rectangle magique normal de dimensions m et n est un arrangement des entiers de 1 à mn dans les cases d’un rectangle, de telle sorte que les m lignes de l’arrangement présentent la même somme, et que les n colonnes du rectangle présentent également la même somme, les deux sommes magiques étant évidemment différentes si m ≠ n.
1. Existe-t-il des rectangles magiques de dimensions m et n si ces deux nombres sont de parités différentes ?
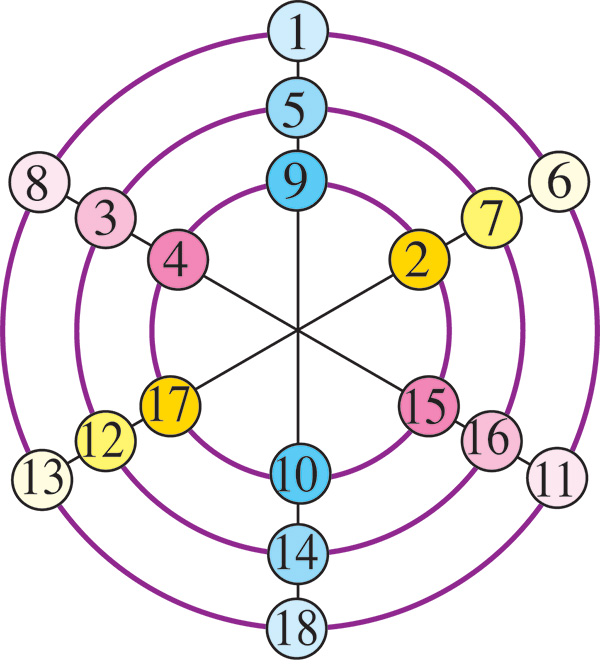
Donnons un exemple avec un rectangle magique 2 × 4. Ce rectangle contient les entiers de 1 à 8, et présente une somme magique égale à 18 sur les lignes et à 9 sur les colonnes.

Après avoir construit un second rectangle magique de dimensions 2 × 4 contenant les nombres entiers de 9 à 16, on peut réaliser une figure magique composée de deux cercles et quatre diamètres. La somme magique sur les cercles est égale à 68 et la somme magique sur les diamètres à 34. On pourrait ajouter le nombre 17 au centre de la figure, ce qui porterait la somme magique des diamètres à 51, sans modifier celle des cercles.
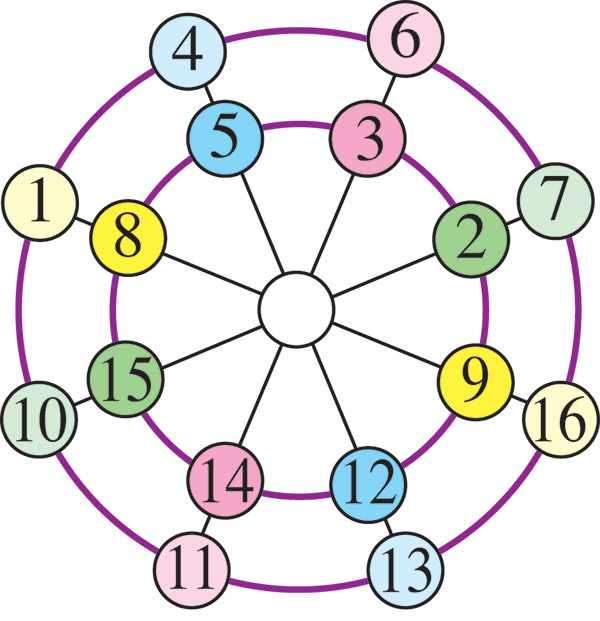
2. Dans une figure magique normale comprenant m cercles et m + 1 diamètres, est-il toujours théoriquement possible, en ajoutant le nombre m2 + m + 1 au centre, d’obtenir la même somme magique sur les cercles et les diamètres ?

