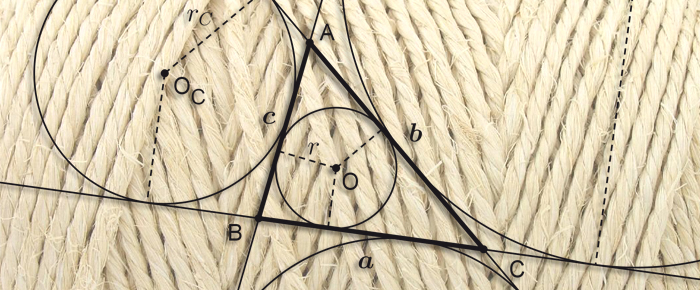
La formule de Héron
Elle nous vient de l'Antiquité et c'est un joyau de la géométrie du plan. Bien plus récente et méconnue que les théorèmes de Thalès et de Pythagore, la formule de Héron permet de déterminer l'aire d'un triangle à l'aide de la seule connaissance de la longueur de ses côtés.
Ce n'est que la partie émergée de la pyramide car cette pépite géométrique se généralise grandement au-delà du triangle. Ainsi, le génial Euler en a trouvé une version sidérante pour le tétraèdre. Brahmagupta puis Bretschneider en ont proposé une variante pour les quadrilatères.
Enfin, à l'instar de son illustre prédécesseur le théorème de Pythagore, la formule de Héron peut donner lieu à des recherches arithmétiques étonnantes, comme celle des « triplets héroniens ». Bienvenue en géométrie !
Ce n'est que la partie émergée de la pyramide car cette pépite géométrique se généralise grandement au-delà du triangle. Ainsi, le génial Euler en a trouvé une version sidérante pour le tétraèdre. Brahmagupta puis Bretschneider en ont proposé une variante pour les quadrilatères.
Enfin, à l'instar de son illustre prédécesseur le théorème de Pythagore, la formule de Héron peut donner lieu à des recherches arithmétiques étonnantes, comme celle des « triplets héroniens ». Bienvenue en géométrie !

LES ARTICLES
Une formule de haut vol
Fabien Aoustin
Vous avez tous appris à vous saisir d'un compas pour tracer un triangle dont on connaît les longueurs des trois côtés. Ces nombres suffisent donc à caractériser un triangle. Mais, à partir de ces seules données, comment en déduire son aire ? C'est l'objet de la formule de Héron.
Un nid à théorèmes
Fabien Aoustin
La formule de Héron frappe les esprits par sa simplicité. Elle est d'autant plus étonnante qu'elle permet d'établir de manière très efficace d'autres résultats tout aussi esthétiques. Elle débouche même sur d'autres problèmes de géométrie passionnants !
En bref : Le Héron de l'espace
Michel Criton et Jean-Jacques DupasLa formule de Héron se généralise aux quadrilatères, aux tétraèdres, mais également à tous les polyèdres, fournissant ainsi de nombreuses applications toujours d'actualité.