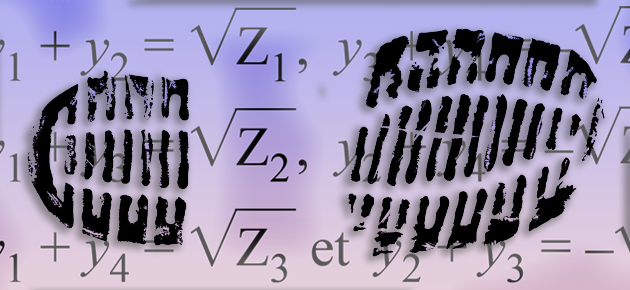Une structure incontournable
Il est difficile d’imaginer l’algèbre sans la théorie des groupes. Pourtant, ce n’est qu’à partir du début du XIXe siècle que la notion se développe, présente implicitement dans les travaux de Lagrange, puis introduite par Galois. D’abord limitée aux seuls groupes des permutations d’un ensemble, la notion s’est peu à peu imposée dans tous les domaines des mathématiques pour étudier non plus seulement les objets, mais aussi les relations entre eux.
La définition formelle d’un groupe n’apparaît qu’à la fin du XIXe siècle. Se développent alors quantité d’outils pour utiliser, répertorier, construire les nombreux exemples de cette structure unificatrice qui déferle sur les mathématiques… et toutes les sciences. Graal ultime, le théorème de classification des groupes finis simples connaît encore des répercussions aujourd’hui.
La définition formelle d’un groupe n’apparaît qu’à la fin du XIXe siècle. Se développent alors quantité d’outils pour utiliser, répertorier, construire les nombreux exemples de cette structure unificatrice qui déferle sur les mathématiques… et toutes les sciences. Graal ultime, le théorème de classification des groupes finis simples connaît encore des répercussions aujourd’hui.

LES ARTICLES
Premier pas vers le concept de groupe
Anne Boyé
Joseph-Louis Lagrange s'est intéressé, dès 1770, à la résolution des équations polynomiales. Il voulait savoir pourquoi les équations de degré 3 et celles de degré 4 étaient résolubles par radicaux. Ce faisant, il s'est intéressé aux permutations sur les racines de ces équations.
L'apport génial de Galois
Daniel Lignon
Après ses travaux sur la recherche des solutions d'une équation du quatrième degré, Lagrange s'est posé la question pour le cinquième degré. Il faut attendre Abel pour savoir que ces équations ne sont pas résolubles par radicaux. Galois donnera une condition nécessaire et suffisante pour qu'une équation de degré quelconque le soit. Ce faisant, il fonde la théorie des groupes.
Les structures quotients
Maxime de Ruelle
L'analyse fine de la structure interne des groupes finis est d'une redoutable difficulté. Que peut-on dire d'un groupe quelconque ? L'idée est de rechercher des sous-groupes, au sein de G, qui vont permettre de reconstituer G en entier. Pour ce faire, les structures quotients sont d'une efficacité imparable.
La classification des groupes finis simples
Daniel Lignon
Simples, les groupes finis ? Cela reste à voir : la classification des groupes finis simples, démarrée il y a plus de cent ans, se poursuit encore aujourd'hui ? par la rédaction d'une démonstration complète ! Celle-ci, commencée à la fin des années 1980, devrait être achevée en 2025. Mais la tâche est ardue ?
Les premières formalisations
Bertrand Hauchecorne
La mort tragique d'Évariste Galois a donné un caractère épique à l'introduction du concept de groupe en mathématiques. Moins connue, la suite est pourtant passionnante, avec à la clé de brillants théorèmes toujours enseignés aujourd'hui. Soixante ans plus tard, la notion de groupe était enfin établie.
En bref : Quelques exemples de groupes
Bertrand Hauchecorne et Daniel LignonLes premiers exemples de groupes qui viennent à l'esprit sont les groupes de nombres. Mais on en trouve dans tous les domaines.
En bref : Le monstre
Daniel LignonLe monstre est un groupe qui possède un nombre d'éléments supérieur au nombre d'atomes sur Terre. Faisons connaissance...